Die Ergebnisse von „Rechenkunststücken“ sollen einen Ausnahmezustand rechtfertigen.
Doch wenn man Tricksen muss, dann bleiben Widersprüche im Zahlenwerk nicht aus, und so verstricken sich denn auch die Verfasser der Studie aus dem Hause des Imperial College in ihren eigenen Modellen und — nicht zu vergessen — auch Ideologien. Ein gewisser Neil M. Ferguson zählt zu den Autoren, er kann als panikmachender Kollege der Deutschen Karl Lauterbach oder auch Christian Drosten eingeordnet werden (1). Es ist bezeichnend, dass man ihn — nicht zum ersten Male (2,3) — unter den Urhebern einer solchen Studie entdeckt. Sebastian Domschke verrät uns im dritten Teil seiner Artikelreihe das Geheimnis der in der Studie „besonders“ bewerteten „letzten Maßnahme“.
Vorab die bisher erschienen Teile:
- Bill Gates und das Imperial College of London — Teil 1
- Bill Gates und das Imperial College of London — Teil 2
Wir haben im zweiten Teil dieser Untersuchung zur Studie des Imperial College — erschienen bei Nature (4) — anhand realer Daten und Rechenvorschrift von R (5,6) den zeitlichen Verlauf der Reproduktionszahl grob für Frankreich abgeschätzt, und dann mit den Deutschen Daten des RKI verglichen, um zu prüfen, ob unser Ergebnis überhaupt plausibel ist.
Das Vier-Phasen-Modell
Das Ergebnis war eine sich ständig verändernde Reproduktionszahl, und dieses Zwischenfazit wird auch von den viel genaueren und professionell erstellten Daten des RKI für Deutschland gestützt. Ohne das jetzt im Detail für die von der Studie modellierten „Infektionszahlen“ nachholen zu wollen, schauen wir uns nun vier Zeiträume genauer an. Wir erinnern uns dabei, dass die folgende Grafik eines von zwei Modellen der Studie wiedergibt (b1):
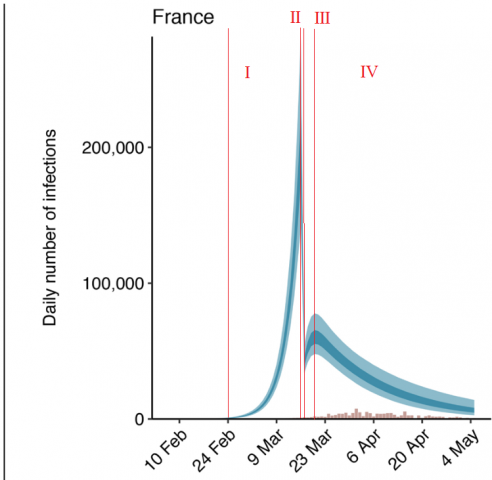
Was sagen diese Phasen aus?
- Phase 1: Starker Anstieg der „Infiziertenzahlen“. Reproduktionszahl R zu Beginn in der Größenordnung 4 bis 5, per Augenmaß tatsächlich konstant
- Phase 2: Einbruch von R auf einen Wert von ungefähr 0,2; gleichzeitig Einbruch bei der Gesamtzahl aller aktuell „Infizierten“ (!)
- Phase 3: R zwar vermindert, aber deutlich über 1 (in grober Näherung 2)
- Phase 4: R sinkt dauerhaft unter 1; nach Abgleich mit den bislang ermittelten Daten auf etwa 0,8
Das vergleichen wir mit dem zweiten Modell der Studie, das wir anfangs des vorigen Teiles bereits kurz vorgestellt hatten, und welches uns die R-Werte verschiedener Phasen (für Frankreich) anzeigt (b2):
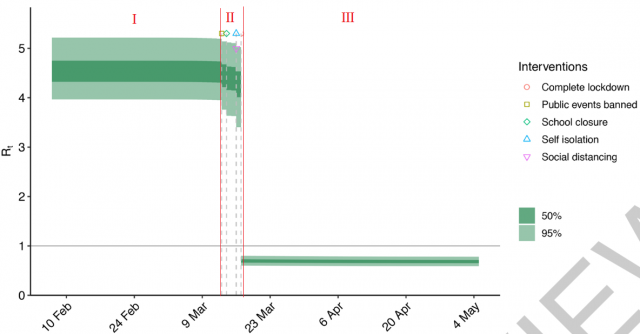
Hier nun können wir allerdings nur noch drei Phasen unterscheiden:
- Phase 1: R-Wert im Bereich 4 bis 5
- Phase 2: R-Wert sinkt unwesentlich in Richtung 4; vorgeblich aufgrund unwirksamer Maßnahmen
- Phase 3: R-Wert konstant unter 1; vorgeblich aufgrund Wirksamkeit des „Lockdowns“
Dazu ist zu vermerken, dass wir in einem Infektionszahlendiagramm (mit den blauen Bändern) per Augenmaß die Phasen I und II (bei den grünen Balken) gar nicht auseinander halten könnten, weil sie viel zu ähnlich aussähen, und dass die Studie völlig kontrafaktisch ganz und gar konstante Reproduktionszahlen annimmt.
Aber das wesentliche ist, dass die ursprüngliche zweite Phase, nämlich der rapide Abfall von R auf Werte von etwa 0,2 und die dritte Phase mit 1 < R < 4 überhaupt nicht mehr auftauchen. Damit sind diese beiden Modellierungen völlig unterschiedlich.
Jetzt stellt sich spontan die Frage, wie der Unterschied in den beiden Modellierungen überhaupt zustande kommt. Konkret diese seltsame Phase 2 bei den Fallzahlen. Wieso bricht R auf einmal auf einen Wert von ~ 0,2 ein, um anschließend wieder über 1 zu steigen und dann abzufallen?
Das liegt jetzt leider an unserer vergleichsweise simplen Art, R zu bestimmen. Ich meine, wenn wir die Methode des RKI verwenden würden, dann ließ sich das Problem lösen, und wir könnten den richtigen R-Wert ablesen, aber leider ist die „komplizierte“ RKI-Methode nichts weiter, als ein mehrtägiger Durchschnitt von dem, was wir gemacht haben (berechnet über vier und sieben Tage), mit dem erklärten Ziel plötzliche Sprünge der Reproduktionszahl zu vermeiden (7).
Damit ist die Methode grundsätzlich nicht geeignet, solch einen Sprung in der Reproduktionszahl abzubilden. Mehr noch: Solche Sprünge zu vermeiden ist ihr erklärtes Ziel. In der Praxis ist das sinnvoll, weil ja eben Reproduktionszahlen nicht einfach springen, sondern in der Regel Ereignisse, wie das Auffinden von vermeintlichen oder tatsächlichen „Hotspots“ massiven Einfluss auf die errechnete, aber eben nicht die reale Reproduktionszahl nehmen können. Und solche Einflüsse möchte man gern kleinrechnen. Für den Modellfall selbst ist uns damit über das Näherungsverfahren des RKI der Zugang verwehrt.
Für das Verständnis entscheidend ist, dass „infizierte“ Personen nicht augenblicklich ansteckend sind, sondern in der Regel erst nach drei bis vier Tagen Krankheitssymptome entwickeln, und damit ansteckend werden (a1). Das heißt, für die „Neuinfektionen“ am 17. März sind nicht die „Infizierten“ der Vortage verantwortlich, sondern jene „Infizierten“ die drei, vier oder fünf Tage zuvor „infiziert“ worden sind. Man gießt dass in eine Verteilung die zeigen soll, wie lange die „Infektion“ desjenigen her ist, der mich angesteckt hat. Denn jeder „Infizierte“ steckt ja im Schnitt Rt Menschen an, was zuweilen mehr als einer ist. Aber zumindestens im Modell wurde jeder „Infizierte“ von genau einem anderen „Kranken“ (zwischen „Infizierten“ und „Kranken“ wird jede Differenzierung stur vermieden) angesteckt
In der Praxis ist das übrigens ebenfalls eine steile These, denn wenn ich mich zum Beispiel für ein ärztliches Gesundheitszeugnis drei Stunden lang in ein mit Grippepatienten gefülltes Wartezimmer setze, und im Anschluss krank werde, wer hat mich denn dann genau angesteckt? Gibt es überhaupt den einen, oder war die Virenkonzentration vielleicht allgemein ansteckend … ?
Die Studie nimmt eine Generationszeit (g) von durchschnittlich 6,5 Tagen an, was bedeutet, dass jemand der mich ansteckt, im Durchschnitt 6,5 Tage zuvor „infiziert“ worden ist (5). Maßgeblich für die Ansteckung von heute sind daher diejenigen „Infizierten“, die sich vor fünf bis acht Tagen angesteckt haben. Und das sind wenigstens vier mal weniger als zuletzt. Deren Reproduktionszahl sinkt jetzt urplötzlich — und zwar von einem Wert etwas über vier — was mehr Neuinfektionen als am Vortag zur Folge hätte — auf einen Wert von ~0,8, was 20% weniger Infektionen als vor 6,5 Tagen bedeutet.
Dieser Effekt erzeugt einerseits diesen gigantischen plötzlichen Abfall der Neuinfektionen am Tag des „Lockdown“, und andererseits auch den moderaten Anstieg bis etwa fünf Tage später. Denn fünf Tage später sind ja dann jene „Infizierte“ für die „Neuinfektionen“ verantwortlich, die am Tag vor dem „Lockdown“ „infiziert“ worden — dem Tag, an dem nach Modellannahme das Infektionsgeschehen sein Maximum erreicht hat.
Es sei an dieser Stelle allerdings darauf hingewiesen, dass der folgende Anstieg bis nach fünf Tagen nicht zu einer erneuten Vervierfachung führt, wie es das Infektionsmodell nahelegt, sondern nur noch zu etwa 1,3 mal mehr „Neuinfektionen“, bezogen auf den Tag nach dem „Lockdown“. Das ist die Wirkung der Verteilung, also die Tatsache, dass eben nicht alle Menschen fünf Tage nach ihrer eigenen Ansteckung jemand Anderen anstecken, sondern manche schon am nächsten, andere erst nach zehn Tagen; laut dem Modell.
In der Studie heißt es dazu lapidar wie irreführend (Übersetzung und Hervorhebung durch Autor):
„Die Zahl der nach unserem Modell geschätzten, täglichen Infektionen fällt direkt nach einer Maßnahme, da wir annehmen, dass alle infizierten Personen durch die Maßnahme augenblicklich weniger infektiös werden. Danach wird, wenn R immer noch über 1 ist, die Zahl der Neuinfektionen wieder ansteigen.“ (4i),
und weiter:
„Aber der Anstieg nach dem Sprung kommt eben nicht durch ein R über 1 zustande, sondern aus dem vorhergehenden modellierten Infektionsgeschehen.“ (4ii)
Soweit die Idee. Praktisch haben wir das Problem, dass wir einen solch schematischen Verlauf schlicht nirgends jemals beobachten. Das heißt, die Studienautoren imaginieren diesen Verlauf der Infektionszahlen aus den Todeszahlen heraus, wo man dies aber mitnichten so beobachten kann. Wie können sie das tun? Und — angenommen das wäre korrekt — warum sehen wir dann solche Verläufe nicht?
Wir fangen mit der zweiten Frage an.
Beim „Lockdown“ (Ausnahmezustand) beobachten wir im Modell diesen beeindruckenden Absturz der Neuinfektionszahlen auf kleiner 20% des Wertes vom Vortage (siehe b1 ganz oben). Aber im Text steht, dass dies unabhängig von der Maßnahme gilt. Ein ähnlicher Sprung müsste sich also auch für die anderen Maßnahmen zeigen. „Leider“ sind die, laut Studie, alle mehr oder weniger unwirksam, wie das folgende Schaubild zeigen soll, welches die relative Verringerung von R durch die verschiedenen Maßnahmen zeigen möchte (b3):
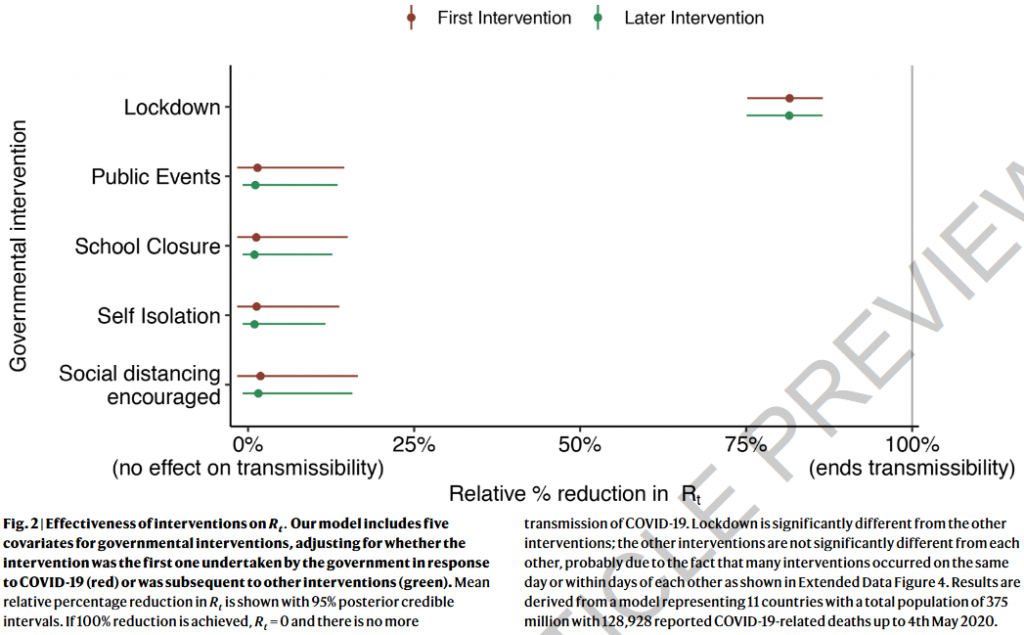
Das erste, was uns hier auffällt, ist, dass sich für die „unwirksamen“ Maßnahmen (Schulschließungen, soziale Distanzierung und so weiter) noch nicht einmal gesichert vorhersagen lässt, ob diese überhaupt einen ausschließlich positiven Einfluss haben könnten, und nicht etwa die Situation vielleicht sogar verschlimmerten. Denn der Vertrauens/Fehlerbereich geht über die 0% Veränderung ins Negative hinaus — was die Grafik übrigens sogar leicht andeutet („0%“ etwas nach rechts versetzt zum Beginn der Rt-Achse). R könnte also durchaus auch steigen, wenn man die Schulen dicht macht, auch laut Studie. Das andere ist, dass die Fehlerbalken sich bei diesen Maßnahmen durchaus auch bis 20% Minderung erstrecken, aber die Durchschnittswerte alle bei zwei bis drei Prozent herumkrebsen. Das ist, gelinde gesagt seltsam. Nebenbei ist die Bildunterschrift irreführend, ich gehe am Schluss darauf ein.
Die Methode „pooling“
Weil die Auswirkungen dieser Maßnahmen — laut Modell — so klein sind, sind die Sprünge in den Diagrammen schwer auszumachen (siehe weiter oben in Bild 2, Phase 2). Die fallen kaum auf. Da aber unsere Augen auf solche Sprünge gut reagieren, sollten sie trotzdem sichtbar sein, wenigstens wenn sie günstig liegen. In der Studie finden sich einige Länder, in denen man erwarten dürfte, wenigstens leichte Sprünge zu finden. Gehen wir die mal durch (b4):
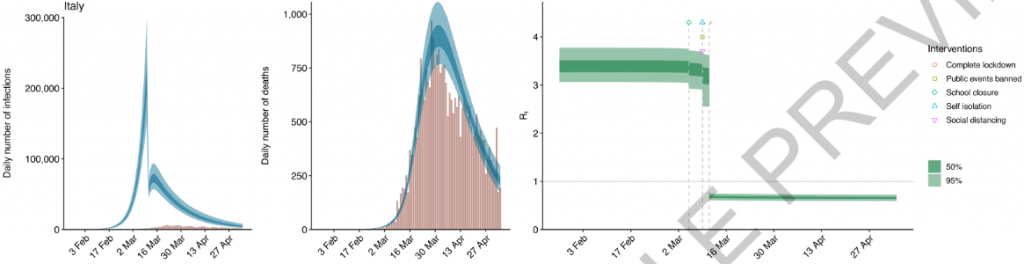
Italien hat — siehe die rechte Abbildung im Bild oben — gleich drei Maßnahmen an einem einzigen Tag durchgeführt. Das sind diese drei Symbole, die ganz rechts auch in der Legende abgebildet sind. Die Maßnahmen addieren sich, was zu einem Sprung im linken Bild von 5 bis 10% führen sollte. Den könnte man sehen. Leider passiert der nur einen Tag vor dem Lockdown, und wäre daher per Augenmaß nur schwer von diesem zu trennen. Ich kann da nichts sehen. Gehen wir zum nächsten Land, Belgien (b5):
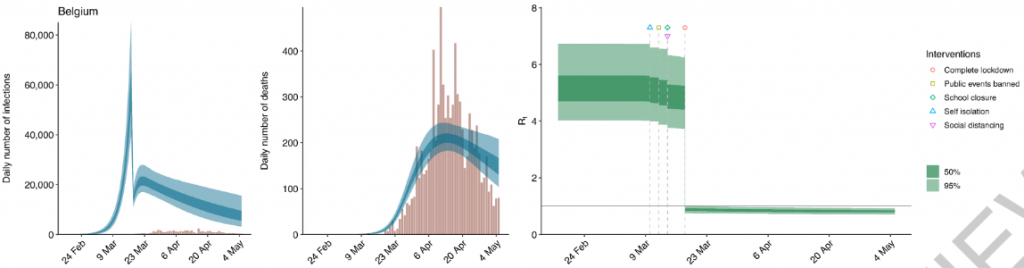
Alle vier Maßnahmen, abgesehen vom „Lockdown“ wurden innerhalb von nur vier Tagen und deutlich vor dem Lockdown verhängt. Ich sehe trotzdem nichts. Aber in Dänemark — wo vier Maßnahmen innerhalb von zwei Tagen gültig wurden, da müsste es doch auffällig sein, oder (b6)?
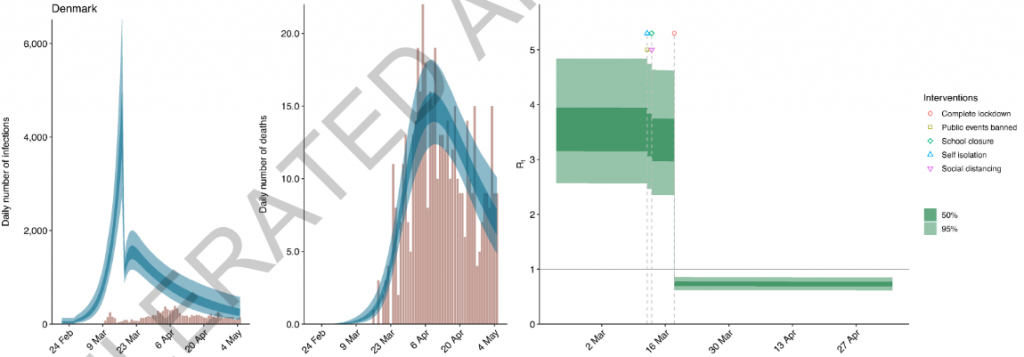
Die vier Maßnahmen sollte man nicht unterscheiden können, den Sprung sollte man also links als einen einzigen deutlich sehen. Nichts. Ein besseres Beispiel als Dänemark findet sich nicht. Wenn wir hier keine Sprünge bei den anderen Maßnahmen (als dem „Lockdown“) erkennen können, dann finden wir nirgends welche. In der Bildunterschrift waren augenscheinlich alle Maßnahmen gemeint. Nachvollziehen lässt sich das nicht.
Es sieht eher so aus, als wäre der „Lockdown“ jedes mal ausdrücklich anders behandelt worden als die anderen Maßnahmen. Und tatsächlich findet sich im Text folgende lustige Passage:
„Rt is modelled as a piecewise constant function that changes only when an intervention occurs. Each country has its own individual starting reproduction number Rt before interventions take place. For all countries, interventions are assumed to have the same relative impact on Rt and are informed by mortality data across all countries. The only exception is that we use partial pooling to introduce country-specific effects of the effectiveness of the last intervention in a country, which is usually the lockdown.“ (4ii)
zu deutsch (Übersetzung durch Autor):
„Rt wird als stückweise konstante Funktion modelliert, die sich immer dann ändert, wenn eine Intervention auftritt. Jedes Land hat seine eigene individuelle Startreproduktionszahl Rt bevor Interventionen stattfinden. Für alle Länder wird angenommen, dass die relative Veränderung einer Intervention auf Rt die selbe ist, und diese werden aus den Sterbezahlen aller Länder gebildet. Die einzige Ausnahme ist, dass wir »partial pooling« benutzen um länderspezifische Effekte der Effektivität der letzten Intervention in einem Land einzuführen (sic!), welche gewöhnlich der Lockdown ist.„
„partial pooling“ ist ein Fachausdruck, dessen Übersetzung nicht in Wörterbüchern nachschlagbar ist, es geht um die gemeinsame Verwendung von Parametern, was hier normalerweise getan wird, während bei der letzten Intervention dieser gemeinsame Parameter um einen zusätzlichen länderspezifischen, also nicht gemeinsam genutzten Parameter ergänzt wird, was mit »partial pooling« bezeichnet wird
Die letzte Maßnahme
Warum man aber für alle Länder je Maßnahme eine einzige Variable nutzt, und nicht etwa für jedes Land und Maßnahme eine Eigene, wird an anderer Stelle erwähnt — nämlich bei „Supplementary Discussion 8. Separate country analyses“ (8). Das Bild dazu ist eine Perle, und ich will es den Lesern nicht vorenthalten (b7):
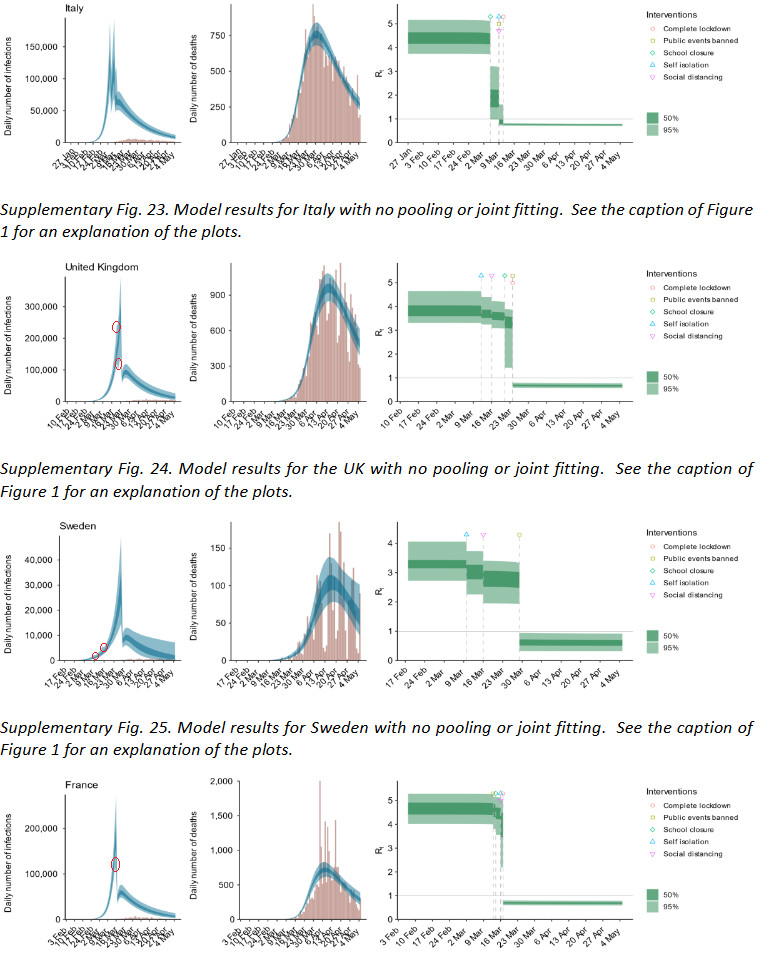
Für den Zeitraum der kleinen, kaum sichtbaren Sprünge in den Grafiken rechts hat der Autor in den jeweiligen, korrespondierenden Grafiken ganz links den entsprechenden Teil der Graphen markiert. Mit der „no pooling“ – Option sind die kleinen Änderungen jetzt gut erkennbar. Man beachte auch die gewaltigen Unterschiede im Maximum der Infektionszahlen, bei Italien immerhin ein Faktor 2. Drei der eigentlichen Diagramme finden sich hier im Text. Das Vereinigte Königreich hat mit „pooling“ ein Maximum über 400.000. Es ergeben sich also durchaus gewichtige Unterschiede.
Dazu heißt es im Text:
„These figures show considerable agreement with the (full and partial) pooled models but the uncertainty is greater in a model with no pooling providing scientific justification for a pooled model.“ (8i)
Vom Autor ins Deutsche übersetzt lautet es:
„Diese Diagramme zeigen beachtliche Übereinstimmung mit den (vollständigen und teilweisen) pooled Modellen aber die Unsicherheit ist größer in einem Modell ohne pooling, was eine wissenschaftliche Begründung für das pooled – Modell liefert.„
Oder für den Unbedarften: Weil uns die Fehlerbalken sonst nicht gefallen, weil diese zu groß wären, benutzen wir die Modelle, bei denen sie durch einen Trick — den des „pooling“ — unscheinbarer werden und die Maßnahme des „Lockdown“ in ihrer länderübergreifend segensreichen Wirkung so richtig zur Geltung bringen. Das nennen die Autoren eine wissenschaftliche Begründung. Eigentlich sollte es nur darum gehen, dass länderspezifische, zufällige Effekte bei der letzten Intervention mit berücksichtigt werden. Warum, das wird tief in den Eingeweiden der Grundlagentexte erwähnt (a2):
The country-specific random effect βm on the last intervention is included to allow for variation between the countries in the effectiveness of the implementation of the interventions.“ (8ii)
Zusammengefasst, schreiben die Autoren hier also, dass die Wirksamkeit der Maßnahmen in allen Ländern als gleich angenommen wurde, weil die Daten dann am besten aussehen. Aber weil die Länder die Maßnahmen unterschiedlich umsetzen, und damit Unterschiede in den Auswirkungen einfach auftreten müssen, führt man bei der letzten, und nur bei der letzten Maßnahme einen Korrekturterm (βm) ein, um all diese Unterschiede auf einmal zu erschlagen. Mit Volker Pispers: „Da geht der Riss mitten durch den Gedankengang. Verschleiert wird er nur durch den Punkt zwischen zwei Sätzen.“ Und die Tatsache, dass diese beiden Sätze nirgendwo in der Studie hintereinander stehen — sondern weit, weit, weit voneinander entfernt, in verschiedenen Teildokumenten der „supplementaries“, macht aus dem Riss einen Spalt, wie er breiter kaum sein könnte.
Zu erwarten gewesen wäre hier, dass einfach von Land zu Land jeweils eine eigene spezifische relative Änderung für R durch den „Lockdown“ — und wirklich auch nur durch den — ermittelt wird. Stattdessen geht es den Verfassern offensichtlich darum, zusätzliche Effekte, nämlich die länderspezifischen Auswirkungen der verschiedenen einzelnen Maßnahmen „einzuführen“ (introduce)! Das führt dann aber zu dem Effekt, den wir in den Diagrammen als Sprung sehen können, und zeitlich ausschließlich dem „Lockdown“ zuordnen sollen.
Die letzte Aussage ist allerdings zu korrigieren, denn diese letzte Maßnahme ist nämlich keineswegs zwingend der ultimative und alle gerettet habende „Lockdown“. Gern hätten es wohl die Autoren der Studie so gehabt. So doch ihre Rechenspielerei dazu führt, dass der letzte Schritt gegenüber den anderen Interventionen besonders groß und beeindruckend — quasi „beweisend“ — wirkt. Das Kriterium ist, wie der Text sagt, dass es die letzte Maßnahme war; „normalerweise“ (normal ist das keineswegs) der „Lockdown“.
Aber es gibt in dieser Studie eine Ausnahme. Ein Land, dessen letzte Maßnahme nicht der „Lockdown“ war. Weil dieses Land keinen „Lockdown“ (Ausnahmezustand) verhängt hat, und das ist Schweden.
Und wie zu erwarten war, verzeichnet auch Schweden einen rapiden Abfall der Neuinfizierten mit der letzten Maßnahme (b8):
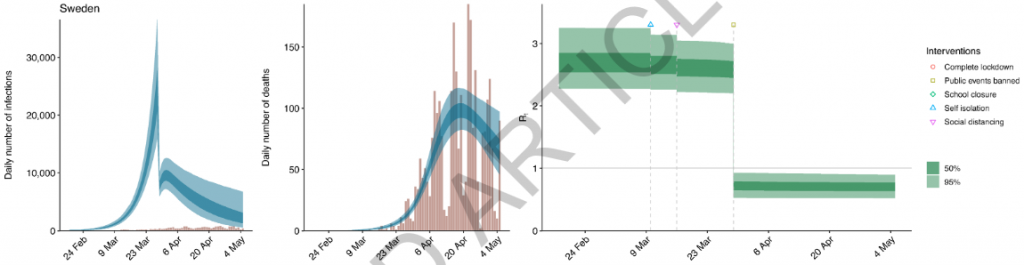
Aber es war eben nicht der „Lockdown“. Es war das Verbot von öffentlichen Veranstaltungen, und wenn man die Maßnahmen einzeln betrachtet, dann gibt es drei Maßnahmen und drei Sprünge (siehe Supplementary, Fig. 25 in Bild b7 weiter oben).
Das Verbot öffentlicher Veranstaltungen — das war die letzte Intervention in diesem Land — hat in Schweden augenscheinlich (nach der Studie) einen Einbruch von R um etwa 70% erzeugt. Warum soll das nur in Schweden so stark gewirkt haben, und wieso sehen wir das im bereits weiter oben gezeigten Schaubild über die Wirksamkeit der Maßnahmen nicht (b3i)?

Der Fehlerbalken von Publik Events (öffentliche Veranstaltungen), und zwar der grüne der für die „Later Intervention“ (letzte Maßnahme) steht, sollte nach rechts aller wenigstens deutlich verlängert sein, im Vergleich zu den anderen. Denn wenigstens in Schweden soll der Effekt ja deutlich sichtbar gewesen sein. Das ist er im Diagramm oben aber nicht. Es scheint ganz so, als hätten diese Zahlen gar nichts miteinander zu tun.
Ich vermute, die Erklärung dafür ist, dass der Sprung in Schweden eben nicht aus der Reduktion von R durch das Verbot öffentlicher Veranstaltungen kommt, sondern eben aus dem Korrekturterm für alle Maßnahmen βm. Und der wird nirgendwo abgebildet, man erfährt nur, dass es ihn gibt.
Man hat hier also offenbar die letzte Maßnahme anders behandelt als die anderen, weil „die letzte Maßnahme“ ein generelles Kriterium ist — im Unterschied zum speziellen Kriterium „Lockdown“, dessen „generelle“ Behandlung man nutzen kann, um die Ähnlichkeit der Verläufe der Todeszahlen in den verschiedenen Ländern aneinander anzupassen, ohne spezifisch zu sagen, man würde den „Lockdown“ anders behandeln, und in Schweden nicht den „Lockdown“ sondern die Großveranstaltungen. Man sieht auch wunderbar, dass dadurch aus mehreren kleinen oder oder nicht ganz so kleinen Sprüngen im Diagramm immer ein einziger großer entsteht, der den „Lockdown“ in seiner Wirkung massiv überzeichnet! Auch diese „Besonderheit“ ist nicht nur dem Verfasser der vorliegenden Abhandlung aufgefallen (9,10).
Das ist harter Tobak. Wenn wir das ernst nehmen würden, würde das bedeuten, wenn man in England nichts anderes gemacht hätte, als das Niesen auf öffentlichen Plätzen zu verbieten, und sonst nichts, dann könnten wir — weil es ja schließlich die letzte Maßnahme war — diese eine einer gesonderten statistischen Auswertung unterziehen, und nachweisen das … ja eigentlich alles.
Wir erinnern uns, dass der Rückgang der Reproduktionszahl R ja schon vor Einsetzen aller Maßnahmen im Wesentlichen abgeschlossen war. Man müsste einfach nur per Definition einführen (introduce), dass diese eine, letzte Intervention einen passenden Einfluss auf irgend etwas hätte. Der Parameter βm stellt dann sicher, dass diese Maßnahme auch den Effekt zeigt, den wir haben wollen, und das muss ein großer, überwältigender Effekt sein. Schließlich muss man ja den Bevölkerungen mit dem „Lockdown“ einen Ausnahmezustand, einen Notstand mit massiven Einschränkungen der Grundrechte schmackhaft machen. Wie unpassend, dass es in Schweden den Ausnahmezustand gar nicht gab.
Nachdem wir jetzt die Modellierung behandelt haben, stellt sich praktisch noch die Frage, warum wir so eine seltsame Grafik in unseren Ausgangsdaten (den Todeszahlen) nicht sehen können. Und das ist sehr einfach zu beantworten. Nehmen wir als Arbeitshypothese an, es gäbe einen solchen Verlauf der Infektionszahlen, dann wird der Anstieg um einen Faktor 4 bis 5 in den Tagen vor dem „Lockdown“ (respektiv der letzten Maßnahme) allein durch die Verteilung der Ansteckungen nach einer Infektion auf einen Faktor 1,3 eingedampft. Danach wird dieser Faktor von 1,3 durch die Verteilung von Infizierten auf mögliche Todesopfer weiter verringert, und es wird schnell klar, dass von diesem Sprung nichts übrig bleiben kann, was man mit bloßem Auge aus dem Diagramm lesen könnte. Das schaffen dann nur noch Modelle. Und die machen das natürlich nur korrekt, wenn sie mit korrekten Prämissen, also den passend kreierten Parametern arbeiten.
Und jetzt können wir zusammenfassen, was notwendig ist, um diesen so seltsam modellierten (!) Verlauf: exponentieller Anstieg, plötzlich massiver Abfall, nachfolgend erneuter Anstieg und schließlich ein flacher Abfall, überhaupt anzutreffen. Dafür benötigen wir zuerst einmal stückweise konstante Reproduktionszahlen. Dauern bestimmte Veränderungen oder Anpassungen von R einen längeren Zeitraum — und länger meint hier nur wenige Tage, maximal die Generationszeit (g) — dann sind solche Auswirkungen wie im Modell grundsätzlich nicht mehr beobachtbar. Was der zeitliche Abfall von R noch übrig lässt, wird mit Sicherheit von den zugrundeliegenden Verteilungen wie Ansteckung, „Infektion“ oder „Infektionssterbezeitpunkt“ überdeckt.
Die zweite wesentliche Bedingung ist ein deutlicher Sprung der Reproduktionszahl, als eine plötzliche Änderung, die nebenbei die Reproduktionszahl von einem Wert über 1 auf einen Wert unter 1 drückt. Beides zusammen ist notwendig. Ein plötzlicher Sprung von R = 1,5 auf R = 0,9 ist natürlich sichtbar, erzeugt aber keinesfalls diesen seltsamen Verlauf des erneuten Anstiegs. Ein Sturz von 5 auf 1,3 erzeugt zwar einen starken Absturz, aber der folgende Anstieg geht im generell immernoch vorhandenen Zuwachs einfach unter. Es ist dieser extreme Sturz der Reproduktionszahlen von 4 oder mehr auf unter 1, der dieses Verhalten erst im Modell sichtbar macht.
Und dieser Sturz wurde — wie wir gesehen haben — mit allen Mitteln herbeimodelliert. Indem alle anderen Maßnahmen als insignifikant abgewertet wurden, indem die Wirkung eines „Lockdown“ in besonderer Weise modelliert wurde, und in dem die Besonderheiten Schwedens aus der Analyse im Wesentlichen herausgetrickst wurden — über den unscheinbaren Terminus „die letzte Maßnahme“.
Zwischenfazit
Es scheint als wäre dies von Anfang an das gewünschte Ergebnis gewesen. Die Maßnahme „Lockdown“ sollte unbedingt effektiv aussehen. Und unter den (modellhaften) Bedingungen, unter denen sie das so weit nur irgend möglich auch tut, sieht dann das Diagramm für die Infektionszahlen so ungewöhnlich aus. Die notwendigen Bedingungen sind zum einen die Art und Weise wie die mathematische Modellierung gestaltet wird und zum anderen einige Annahmen über den Verlauf der Pandemie.
Man sollte sich auch klar machen, dass die Vertrauensbereiche hier allesamt Makulatur sind. Sie hängen an den sehr konkreten Annahmen über den Verlauf, die sich überhaupt nicht zwingend aus irgend etwas ergeben, sondern höchst spekulativ sind (und ja eigentlich erst bestimmt werden sollten), den Wirkungen der Maßnahmen, und eben auch den mathematischen Parametern die gewählt werden. Nicht so sehr hängen sie dabei an der Datenbasis, obwohl allein diese für sich betrachtet selbst schon größte Unsicherheiten mitbringt. Diese Unsicherheit der Datenbasis wurde hier aber generell weitgehend ignoriert.
Die wichtigsten Annahme ist sicherlich, dass das Virus völlig neu ist, und deshalb in der Bevölkerung bis dato nicht vorkam. Nur dann könnte man irgendwie wenigstens augenscheinlich bei explosiv steigenden Testzahlen aus den absolut gemessenen positiven Tests auch in gleicher Weise steigende Fallzahlen erwarten. Was ja die Basis ist, auch für die RKI-Bewertung von ursprünglichen Reproduktionszahlen von 3 (RKI) bzw. 4 bis 5 (ECDC).
Das ist aber extrem fragwürdig, weil das bedeuten würde, dass man in jedem Moment gerade zufällig genau so viele Tests pro Tag zu produzieren und auszuwerten in der Lage ist, wie benötigt werden, um das Infektionsgeschehen adäquat abzubilden, während man die Testkapazitäten ständig massiv erweitert, und dass man — ganz ohne Test — auch in der Lage ist, genau diejenigen Individuen zu identifizieren, die man testen muss, um das zu gewährleisten. Das ist Wunschdenken aber keine Wissenschaft.
Nimmt man diese Annahme eines „neuartigen Virus“ weg, und geht davon aus, dass dieses Virus schon längere Zeit in der Bevölkerung umgeht — und wir reden hier nur von zwei bis drei Monaten — dann ist nicht die absolute Zahl an positiven Tests, sondern die relative (!) Zahl an positiven Tests entscheidend für die Berechnung der „Ausgangswerte“ für R, und die sehen dann bereits ganz anders aus. Das ist dann auch schon kein R0 mehr, sondern ein Rt für einen unbekannten Zeitpunkt während der Pandemie, weil sich der Anfang aus den Daten nicht mehr bestimmen ließe. Damals gab es schlichtweg keinen Test; noch besser wären freilich sowieso repräsentative Tests, die es aber nach wie vor nicht gibt.
Aber mit solchen Fragen setzt man sich hier eben nicht auseinander. Stattdessen wird die Frage nach der Evidenz allein danach beantwortet, ob die Fehlergrenzen im Rahmen dieser oder jener mathematischen Modellierung (die sich in ihren Parametern, aber nicht in ihren Grundannahmen unterscheiden) des selben realen Sachverhalts kleiner oder größer ausfallen.
Danke Sebastian, bitte bleiben Sie schön aufmerksam, liebe Leser.
Anmerkungen und Quellen
(Allgemein) Dieser Artikel von Peds Ansichten ist unter einer Creative Commons-Lizenz (Namensnennung – Nicht kommerziell – Keine Bearbeitungen 4.0 International) lizenziert. Unter Einhaltung der Lizenzbedingungen kann er gern weiterverbreitet und vervielfältigt werden. Bei Verlinkungen auf weitere Artikel von Peds Ansichten finden Sie dort auch die externen Quellen, mit denen die Aussagen im aktuellen Text belegt werden. Die Rechte des Autors Sebastian Domschke bleiben davon unbelassen. Redaktionelle Einarbeitung durch Peds Ansichten. Letzte Bearbeitung: 19. Mai 2023.
(a1) Hier wird die Glaskugel in den Modellierungen des Imperial College ein weiteres Mal bemüht, denn die „Infektionstheorie“ wartet bis zum heutigen Tag auf die wissenschaftlichen Belege, die sie erst zu einer Theorie machen würde. Die Annahme, dass Menschen sich innerhalb eines gesunden, hygienischen Milieus gegenseitig „infizieren“ ist in keiner Weise nachgewiesen.
(a2) In der endgültigen Fassung der Studie des Imperial College sind diese Erläuterungen zu den eingesetzten Modellparametern nicht mehr enthalten.
(1) 27.03.2020; MDR; Stimmen die Zahlen möglicher Corona-Todesopfer?; https://www.mdr.de/wissen/corona-todeszahl-ferguson-studie-100.html
(2) 12.05.2009; Spiegel; Forscher befürchten zehnmal höhere Zahl von Infektionen; https://www.spiegel.de/wissenschaft/mensch/schweinegrippe-forscher-befuerchten-zehnmal-hoehere-zahl-von-infektionen-a-624285.html; aus dem Artikel: „Fergusons Team unterstützt in seinem »Science«-Beitrag ausdrücklich die Linie der Weltgesundheitsorganisation WHO, die auf der Pandemie-Warnskala die Stufe fünf von sechs ausgerufen hat. Bei den vorliegenden Ausbreitungszahlen sei diese Entscheidung angemessen, so die Forscher. »Es ist ein Virus, das mit ziemlicher Sicherheit eine globale Epidemie auslösen wird«, sagte Ferguson dem Onlinedienst »Nature News«„.
(3) 24.01.2002; NIH; Neil M. Ferguson, A C Ghani, C A Donnelly und weitere; Estimating the human health risk from possible BSE infection of the British sheep flock; https://pubmed.ncbi.nlm.nih.gov/11786878/
(4) 08.06.2020; Erstveröffentlichung: 30.03.2020; Imperial College; Estimation the effects of non-pharmaceutical interventions on COVID-19 in Europe; Seth Flaxman, Swapnil Mishra, Neil M. Ferguson und weitere; https://www.nature.com/articles/s41586-020-2405-7/figures/6
(4i) Originaler Wortlaut in Abbildung 1 der Studie: „The number of daily infections estimated by our model drops immediately after an intervention, as we assume that all infected people become immediately less infectious through the intervention. Afterwards, if the Rt is above 1, the number of infections will start growing again.„
(5) https://de.wikipedia.org/wiki/Standardisierung_(Statistik)#Herleitung_der_mathematischen_Formel; abgerufen: 15.10.2020
(6) 26.10.2017; RKI; Antworten auf häufig gestellte Fragen zur Pest; https://www.rki.de/SharedDocs/FAQ/Pest/FAQ_Liste.html
(7,7i) https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Projekte_RKI/R-Wert-Erlaeuterung.pdf?__blob=publicationFile
Zur Erklärung: Im Unterschied zur Studie, die sich gaaaaaaaaanz genau an das mathematisch methodische Prozedere hält (soweit ich das beurteilen kann; was übrigens auch heißt, dass sie einen einzelnen Menschen nicht zählen sondern aufintegrieren) ist es dem RKI auch zu mühsam, mit Verteilungen zu arbeiten. Deswegen nehmen die einen Zwischenwertsatz, der besagt, dass, wenn man verschiedene ‚R‘ ausrechnet aus den Tageswerten, E(t)/E(t-1), E(t)/E(t-2), E(t)/E(t-3) … E(t)/E(t-i) … E(t)/E(t-n) … es irgendwo einen geben muss, der dem korrekten R-Wert entspricht. Im Dokument heißt es „Unter der Annahme einer konstanten Generationszeit (g) und eines konstanten seriellen Intervalls …“. Und das soll dann der Fall sein, wenn i = g die Generationszeit wird. Das hört sich plausibel an, scheint aber nicht zu funktionieren, wenn man es konkret nachrechnet. Denn das würde vorraussetzen, dass egal, welchen konkreten Verlauf wir finden, immer das selbe g=i zur korrekten Reproduktionszahl führt. Dem ist aber nicht einmal dann so, wenn R über lange Zeiträume konstant bleibt.
(8,8i) Supplementary Discussion 8. Seperate country analyses; https://static-content.springer.com/esm/art%3A10.1038%2Fs41586-020-2405-7/MediaObjects/41586_2020_2405_MOESM1_ESM.pdf; S. 21, S. 6 (5i)
(9) 21.06.2020; Climate Etc.; Nic Lewis; Did lockdowns really save 3 million COVID-19 deaths, as Flaxman et al. claim?; https://judithcurry.com/2020/06/21/did-lockdowns-really-save-3-million-covid-19-deaths-as-flaxman-et-al-claim/; siehe insbesondere Kap. „The Sweden problem“
(10) 04.06.2020; MEI; Peter St. Onge; Gaël Campan; The Flawed Covid-19 Model That Locked Down Canada; https://www.iedm.org/the-flawed-covid-19-model-that-locked-down-canada/
(b1) Imperial College; Modell zur Darstellung der Reproduktionszahl in Abhängigkeit von der Einführung landesweiter Ausgangssperren („Lockdown“), phasenweiser Verlauf
(b2) Imperial College; Modell zur Darstellung der Reproduktionszahl in Abhängigkeit von der Einführung landesweiter Ausgangssperren („Lockdown“), phasenweiser Verlauf des R-Wertes
(b3,b3i) Imperial College; Modellierung zur vorgeblichen, allgemeinen Wirksamkeit der Maßnahmen im Rahmen nichtmedizinischer Intervention
(b4) Imperial College; angebliche Wirksamkeit der Maßnahmen im Rahmen nichtmedizinischer Intervention in Italien
(b5) Imperial College; angebliche Wirksamkeit der Maßnahmen im Rahmen nichtmedizinischer Intervention in Belgien
(b6) Imperial College; angebliche Wirksamkeit der Maßnahmen im Rahmen nichtmedizinischer Intervention in Dänemark
(b7) Imperial College; angebliche Wirksamkeit der Maßnahmen in Italien, Großbritannien, Schweden und Frankreich; Darstellung mit „no polling“ – Effekt; Supplementary Discussion 8. Seperate country analyses; https://static-content.springer.com/esm/art%3A10.1038%2Fs41586-020-2405-7/MediaObjects/41586_2020_2405_MOESM1_ESM.pdf; Bild 23 bis 26, S. 20
(b8) Imperial College; Studie; Wirksamkeit der Maßnahmen; Schweden
(Titelbild) Grafik, Diagramm; Autor: Mediamodifier (Pixabay); 23.12.2017; https://pixabay.com/de/illustrations/grafik-diagramm-wachstum-3033203/; Lizenz: Pixabay License
Vielleicht etwas OT, aber zum großen Ganzen:
Den Herrschenden geht und ging es zu allen Zeiten – von den Pharaonen über das Gottkaiser- und Papsttum, der Hitler-Verehrung – bis zur heutigen Zeit der Wissenschaftsgläubigkeit immer nur um eines:
ein dominantes Weltbild einzuführen, dessen oberste Repräsentanten und Vertreter von ihnen, den Herrschenden, ausgewählt und bestimmt werden können, um ihre Glaubens- und Meinungsführerschaft durchzusetzen.
Wenn man das versteht, versteht man auch die Gemeinsamkeit scheinbar unterschiedlicher Aktivitäten wie die auf PSIRAM, von so genannten „Skeptikern“ von Organisationen wie GWUP, natürlich der Hauptmedien, dem ÖRR, der etablierten Politik, den „Mythen-Jägern“, „Fake News-Jägern“, „Correctiv“, , „Anti-Verschwörungstheoretikern“, Debunkern, Lesch, Yogishwa, Mai Ty,
man versteht diese ganze scheinbar zersplitterte Bemühungen als einem Ziel verpflichtet: eine einzige, verbindliche, unangefochtene Welterzählung zu schaffen, die für alle gültig sein soll, zwischen Zugehörige und Abtrünnige unterscheidet, eine monopolar Sicht mit dem Alleinstellungsmerkmal der angeblich einzig wahren Wahrheit reichweitenstark durchzusetzen.
Die Herrschenden besitzen das Monopol über das Denken der Beherrschten, indem sie die Autoritäten einsetzen, die die alleinig gültigen Wahrheiten definieren: früher die Kleriker, heute die Wissenschaftler.
Aber während früher immerhin noch unterschiedliche Religionen gegeneinander standen, gibt es heute nur noch die eine, globalisierte Wissenschaftsgemeinschaft. Der absolute Monopol der gültigen Wahrheiten.
Das einzige Ziel ist nicht etwa Fortschritt, richtige Analyse, Wahrheitsfindung – sondern einzig und allein dominante Autoritäten zu setzen, die unumstößliche Wahrheiten verkündigen können wie etwa die, dass aktuell eine tödliche Pandemie herrsche.
() https://youtu.be/EGJ1jcuDS_I
KaiserTV: „maiLab liebt die Technokratie“
‚eine einzige, verbindliche, unangefochtene Weltordnung zu schaffen‘?
Also das ist mir ein wenig unkonkret. Und außerdem so monolithisch. Da macht man ja wieder aus vielem eines.
Vielleicht ist es Hilfreich, selbst verschiedene widersprüchliche Narrative (die Teilaspekte dieser ‚unterschiedlichen Aktivitäten‘ beschreiben) nebeneinander stehen zu lassen, und selbst dann noch, also wenn sie sich gegenseitig widersprechen, beide gleichzeitig als Grundlage eigenen Handelns zu nutzen.
Das große ´Problem der Wissenschaft heute ist tatsächlich die Religiösität. Ob ich einen Prister ausbilde, der dann befugt ist, die Bibel zu lesen, oder einen Wissenschaftler ausbildem der dann befugt ist, die Naturgesetze zu interpretieren – es hat sich im Grunde genau gar nichts geändert.
Und genau das ist auch die Motivation hinter dieser Serie. Es geht darum, dass jeder die Möglichkeit bekommt sich selbst zu bilden. Selbst nach Antworten zu suchen. Und eben nicht zu akzeptieren, dass uns Experten vorexerzieren, was wir denken dürfen, und was nicht.
🙂
Das Ziel ist meiner Meinung nach weniger eine einheitliche Weltsicht zu schaffen (die bildet sich dann höchsten heraus) sondern vor allem, eine möglichst homogene und (über Geld, Ehren und Schmeichelei) beeinflussbare Gruppe von weitgehend gleich sozialisierten und ähnlich motivierten Kreis von Menschen zu haben, die aufgrund von deren Ansehen und Einfluss den Diskurs bestimmen. Diese Leute können sich in Details völlig spinnefeind sein und sonst wie wild zoffen und gegenseitig auszustechen versuchen. Entscheidend ist, einen Pool zu besitzen, aus dem für den Fall (wie jetzt mit Corona) Personen rekrutiert werden können (wie jetzt Wieler, Drosten, Ferguson, Fauci, …), um eine bestimmende, nützliche, herrschende Meinung zu generieren.
Das nur zur Verdeutlichung meines Ansatzes.
… übrigens will ich in keiner Weise Ihre Bemühungen kleinreden, Herr Domschke. Vielmehr haben Sie mich eben zu den weitergehenden Gedanken angeregt. Zum Kern-Thema selbst (also die untersuchte Studie und deren Wert) kann ich aber nicht soviel beitragen. Da sind mE sicherlich vor allem Fachleute auf diesem (und verwandten) Gebiet(en) gefragt.
Bitte spar dir den Herrn. Ich bin kein Herr, und will auch keiner sein. Im Zweifel nicht einmal mein eigener.
Was hält dich denn davon ab, dich mit der Studie selbst zu beschäftigen oder eben etwas beizutragen?
Für mich ist „Herr“ oder „Frau“ die Konvention bei der Anrede – sonst nichts. Also nicht übel nehmen, bitte.
Viel einfacher: Der Vertrauensverlust in die Politik ist so groß, dass man jetzt „die Wissenschaft“ als Indirektionsebene für Herrschaftspolitik benutzt. Der gute Ruf der Wissenschaft soll den schlechten Ruf der Politik kompensieren.
Wissenschaft hat diesen guten Ruf ja noch, übrigens zu unrecht. Die Falschmünzereien „der Wissenschaftler“ hatte bereits Nietzsche (19.Jhdt) in seinen Schriften erwähnt.
Die Wissenschaft ist/war korrupt und wurde durch Murksel-Politik auch noch korrupter gemacht. Ich erwähne nur das Thema Drittmittelfinanzierung.
Auch witzig, kürzlich berichtet eine Medizinstudentin über die Benennung der Hörsäle an ihrer Uni: Sie sind nach Pharmafirmen benannt. Noch Fragen?
Zu MaiFailedLab, Lescherlich & Konsorten: Propagandahuren, weiter nichts. Die Korruption spült zum Schluß einfach nur noch die widerlichsten Charaktere nach oben. Chemikerinen, die sich im Labor die Stirn (und wahrscheinlich auch den Kopf) verbrannt haben gehören auch dazu.
Solch unfähigen Leute hat man glücklicherweise nicht in die Unternehmen gelassen. Umso trauriger das solche „Kapazitäten“ nun bei einem Großbetrug mithelfen.
Der „Wissenschaftsjournalismus“ zeichnet sich heute durchgängig in einem Merkmal eindeutig aus: Wissenschaft wird als ein eigenen abgeschlossene Raum dargestellt, in dem es Disput und Streit gibt, den Kampf um die richtige Theorie, die bessere Hypothese.
Aber, wenn man drauf drückt auf diesen Raum, dann quölle nur Wahrheit und reinste Tatsachenbeschreibungen heraus wie Senf, aus der Senftube.
Das draufdrücken auf diesen heiligen „Wissenschaftsraum“ würde durch den Druck der Öffentlichkeit verursacht, der ja zu einem übergroßen Teil diesen Wissenschaftsbetrieb finanziert und daher ein Recht auf ein Ergebnis („Senf“) habe.
Das dumme an dieser Darstellung ist, dass das hinten und vorne nicht stimmt. Zb dringen aus der Öffentlichkeit Erwartungen in diesen „Wissenschaftsraum“ ein. Die werden zB durch Politiker formuliert, die Gelder verwalten und verteilen können. Damit ist dieser Wissenschaftsraum dem Druck ausgesetzt, nach außen seine inneren Zweifel als Wahrheit zu kommunizieren (aus Theorien wird sicheres Wissen gemacht; wenn es der Wissenschaftler selbst nicht so formuliert, so macht es der Wissenschaftsjournalist), und diese Kommunikation wirkt wieder auf den Wissenschaftsraum zurück (zB über Schüler, die mit Voreinstellungen (zB über die Existenz von „Schwarzen Löchern“) dann Studenten werden).
So werden dann aus Hypothesen ohne wissenschaftlich eindeutigen Fortschritt auf die Dauer „wissenschaftliche Wahrheit“ aus dem schlichten Grund verstärkender Feedback-Schleifen. Die Bevölkerung würde sonst schlicht die ungeheuren Kosten dieses Apparates und dessen Eskapaden (LHC, LIGO, Fusionsforschung, Neutrino-Experimente wie Grand Sasso, Superteleskope, …) nicht mehr einsehen wollen.
Das hier sollte unbedingt eine weite Verbreitung finden. Es ist ein deutlicher Hinweis darauf, wie es zu den hohen Sterbezahlen, hier für Frankreich, im Frühjahr kam. Der Text auf Seite 5 der Patientenzeitschrift Klinikum Kulmbach ist erhellend in zwei Hinsichten:
– massive Intubierung von Corona-Patienten (und daher entsprechender Medikamentenbedarf), die Intubierung ist heute als Fehlbehandlung bekannt
– künstliche Verknappung von Medikamenten für Nicht-Corona-kranke Patienten
https://www.klinikum-kulmbach.de/fileadmin/user_upload/Patientenzeitschrift/web_UNSER_KLINIKUM_Juni_2020.pdf
Dank an einen Foristen auf corodok
https://www.corodok.de/frankreich-todeszahlen-steigen-langsam/
… und in Ergänzung, zur Vertiefung ein weiterer Hinweis „Über Bande“ (aus Indien, über Frankreich)
https://www.rubikon.news/artikel/die-macht-des-wissens
„Dennis Rancourt, ein angesehener Physikprofessor an der Universität Ottawa, und sein Team schreiben in einem im August 2020 veröffentlichten Forschungsbericht, dass die übertrieben strikten Quarantänemaßnahmen, die in Frankreich angeblich zum Schutz der Bevölkerung vor Covid-19 durchgesetzt wurden, zu landesweit 30.200 Todesfällen in den Monaten März und April führten. “
Die Hinweise, dass die „Anti-Covid-Maßnahmen“ selbst für die Übersterblichkeit verantwortlich sind, sind überdeutlich.
Also wenn ich mir die Grafiken (aus der Studie des Imperial College) ansehe, kann ich mir nur an den Kopf greifen. Das ist doch nur peinlich. Und offensichtlich völlig aus der Luft gegriffenes Zeugs …
mit solchen “Studien” und Modellen kann man doch beweisen, was man gerade will …
Uns wird ja dauernd suggeriert, dass es bei dem Ganzen um die Klärung wissenschaftlicher Fragestellungen ginge. Das ist aber überhaupt nicht der Fall. Tatsächlich geht es um eine reine Glaubensfrage. Daher ist auch das Eingehen auf scheinbare wissenschaftliche Begründungen letztlich zwecklos. Diese Studien begründen ja nicht den Glauben an ein gefährliches Virus, sondern diese Studien entstehen AUS DEM GLAUBEN an ein gefährliches Virus (bzw. aus dem Wunsch, solchen Glauben zu verbreiten).
Wenn wir wissenschaftlich vorgehen, so stellen wir fest,
_ dass wir nicht sicher wissen, ob das Covid-19-Virus (sofern es überhaupt existiert) im unterstellten Sinn neuartig ist (es sich also nicht um eine gängige Mutation von Corona-Viren sondern um ein dramatisch in seinen Eigenschaften ganz anderes Virus, vielleicht von Tier auf Mensch übergesprungen, handelt). Und „nicht sicher wissen“ bedeutet hier: minimalste, ja tatsächlich keinerlei Evidenz
_ dass wir nicht sicher wissen ob die Anfang diesen Jahres vielerorts verzeichneten Übersterblichkeiten (allerdings im Rahmen durchaus üblicher Schwankungen der Sterblichkeit) wie behauptet auf das Covid-19-Virus oder aber auf andere Faktoren zurückzuführen ist (und die Hinweise mehren sich, dass zumindest ein nicht unerheblicher Teil der Übersterblichkeit auf „Anti-Covid-19-Maßnahmen“ zurück zu führen sind)
_ dass wir eigentlich inzwischen sogar relativ sicher wissen, dass Maßnahmen wie „Lockdown“, Kontaktbeschränkungen, Maskentragen, etc nichts, aber auch garnichts an der Dynamik einer Erkältungsviren-Epidemie ändern
Wenn man das sieht, stellt man fest, dass die ironische Bezeichnung „Zeugen Coronas“ treffender ist, als man im ersten Moment annimmt: es handelt sich tatsächlich um einen unter der Behauptung von Wissenschaftlichkeit ausgerollten Glauben.
Diese Prognose-Wissenschaften dürften garnicht als Wissenschaften gehandelt werden. Man kann die Realität nicht annähernd genau genug modellieren und simulieren um für so komplexe Vorgänge wie Epidemie-Ausbreitung oder generell jegliche Lebensäußerung, die Zukunft prognostizieren zu können. Simulieren und Modellieren ist die Technik der wissenschaftliche verbrämten Glaubensverbreitung. Bei hinreichend komplexen Simulationen und Modellierungen kommt immer nur das raus, was man hineingesteckt hat: seine eigenen Vorurteile.
Und das alles wissen die Damen und Herren, die uns das Einbrocken, auch ganz genau!
… und hier noch gleich ein andere, wissenschaftliche Stimme („Derzeit ist Ranjan Assistenzprofessor an der Rabindranath Tagore School of Languages and Cultural Studies der Universität Assam.“) zu dem Modellierungs-Wahn:
„Prof. Neil Fergussons Prognosen zu den Covid-19-Todesfällen basierten beispielsweise auf einem statistischen Code, der von Computern ausgewertet wurde. Die Vorhersage auf Basis dieses Codes legitimierten den Lockdown, der Hunderttausende vermeidbare Todesfälle in Großbritannien, Amerika, Indien und in der übrigen Welt verursachte; drängte Millionen Menschen in Arbeitslosigkeit und Armut; beraubte sie ihrer Grundrechte und machte digitale Überwachung zur neuen Normalität.“
„Spätere Studien zeigten jedoch, dass der verwendete Code 13 Jahre alt, simpel und irrelevant ist. Der Code lieferte unterschiedliche Ergebnisse, wenn er von verschiedenen Personen genutzt wurde (22).“
https://www.rubikon.news/artikel/die-macht-des-wissens
Das ist dann noch schlimmer, als ich angenommen habe: nicht einmal ernsthafte Arbeit würde dann hinter dem Wahnsinn stehen. Blenden und Hochstapeln, Lügen, Betrügen und Täuschen, Relotius-Arbeiten sind die Mittel diesen Irrsinn anzutreiben.
… und in Ergänzung zu meinem letzten, noch nicht veröffentlichten Kommentar:
So wie das Relotuis-Prinzip in den Medien funktioniert hat, so funktioniert das auch in der Wissenschaft der heutigen Zeit.
Rezept: identifiziere eine Vorstellung, die einflussreiche Kreise (heute muss man besser sagen: der einflussreiche Kreis – denn es gibt dort keine Diversität mehr) gerne bestätigt sehen würden, setze ein Forschungsprojekt auf, dessen Ergebnisse so hingebogen/ausgelegt werden können, dass es die gewünschte Vorstellung bestätigt, und schreibe dann die entsprechende Studie.
Aktuell läuft zB die Forschung nach „Gravitationswellen“ exakt so ab. Dort müssen schon alleine deshalb positive Ergebnisse IRGENDWIE hervorgebracht werden, weil inzwischen Milliarden an Euro und Dollar dafür verbrannt worden sind.
Warum müssen „Gravitationswellen“ auf Teufel komm raus bewiesen werden? Weil keine Zweifel an der reinen Wahrhaftigkeit unserer heutigen Wissenschaften aufkommen dürfen. Die Vorhersagen von „Gravitationswellen“ erzwingen inzwischen deren „Bestätigung“. Alles andere wäre als dramatische Kontrollverlust der einflussreichen Kräfte zu werten. Das kann und darf unter keinen Umständen eintreten! Dazu sind alle Mittel recht bis hin zum offenen Betrug (künstliche, betrügerische Injektion von Signalen in die Detektoren).
Gelegentlich fasse ich mehrere Ihrer Kommentare in Einen zusammen.
Grüße, Ped
Ich betrachte das Ganze weniger unter einem fachspezifischen sondern eher unter einem soziologischen Blickwinkel.
Und da lässt sich die Verwandtschaft von klerikaler Herrschaft und wissenschaftsgestützter Herrschaft sehr gut herausarbeiten.
Nehmen wir das klerikale System zB zu Zeiten von Galileo und unseren heutigen akademischen Wissenschaftsbetrieb im Vergleich. Beides sind hierarchisch strukturierte Systeme.
Für beide gelten, dass nicht unbedingt die Personen, die besonders gottgläubig/wissenschaftsbereichernd unterwegs waren/sind, die wichtigen Positionen wie zB Bischofsamt/Dekanate einnehmen, sondern die Personen die besondere charakterliche Eingeschaften mitbringen. Als da sind: gutes Gespür für Wünsche und Anforderungen der Höhergestellten, Standesdünkel, Gespür für Codes und Abgrenzungsriten, von Zweifeln ungetrübtes Auftreten, Manipulationsvermögen, Durchsetzungsvermögen, vielleicht Charisma, zumindest Eindruck erweckend (möglichst groß, starke Stimme, Phlegma, Sicherheit, …) große Freiheit bei der Wahl der Mittel haben (eine gewisse Amoralität also, bzw. zumindest hohe Flexibilität in diesem Bezug), vielleicht auch ein Stück weit Selbsstbetrug und Selbstüberhebung ihr Eigen nennen, etc.
Es ist sicher und rein menschlich bedingt anzunehmen, dass eben diese eigenen Charaktere in jedem mehr oder minder hierarchisch organisierten System nach oben steigen werden. Und nach kurzer Zeit (der Existenz eines solchen Systems) greifen die Mechanismen der Seilschaften: Personen erkennen ander Personen, die ihnen zunutze sind, und helfen sich gegenseitig zumindest so lange, so lange sie nicht unmittelbare Konkurrenz befürchten müssen. Und nun nehmen man nur noch vermögende (Geld, Einfluss, Macht besitzende) Gruppen dazu, die diese Strukturen ausnutzen und zu ihren Gunsten beeinflussen wollen.
Und schon haben wir das Papsttum/unseren heutigen Wissenschaftsbetrieb mit „Päpsten“ in jeder Fachrichtung, die Dogmen vorgeben und für die Nachstrebenden die Richtung weisen, andere Richtungen abwürgen, Zweifel an Dogmen bestrafen, Karrieren fördern oder verunmöglichen, …
Das Prinzip ist immer „es kann letzlich nur einen geben“: nur einen Unfehlbaren(Papst)/nur eine Wahrheit (in einer bestimmten Fachrichtung).
Wissenschaft ist eigentlich genau das Gegenteil. Wissenschaft ist der ständige Diskurs, der dauernde Zweifel, der ständige Umsturz. Aber genau das soll ja heute Wissenschaft nicht sein. Vielmehr wird heute (zumindest der Masse) Wissenschaft als Hort letztendlicher Wahrheiten verkauft. Was man heute noch nicht (genau) wisse, würde man morgen sicher wissen. Aber im Prinzip habe man die letzten Wahrheit schon entdeckt. Es gälte nur noch die übrigen (meist unwichtigen) Puzzelteile in das große, sich ja deutlich abzeichenden Ganze einzufügen. So wird heute Wissenschaft den „Gläubigen“, den Aufschauenden, den Überwältigten, den „Unwissenden“ verklärt.
Ja, das ist meine Sicht. Und dass viele, die selbst im Wissenschaftsbetrieb stehen damit nicht glücklich sind, ist mir auch klar.
Mal ein kleiner, virologischer Abstecher-Versuch: Laut „Fachleuten“ (Herr Drebbin hier)
https://www.heise.de/forum/Telepolis/Kommentare/US-Studie-Vermehrte-Fahrten-zwischen-Landkreisen-erhoehen-Corona-Infektionszahlen/Da-seit-Mai-Virenkulturen-vom-CDC-allen-Forschern-zu-Verfuegung/posting-37617073/show/
wäre ja SARSCOV2 seit Mai kultiviert und isoliert (ohne jetzt auf die zeitlichen Ungereimtheiten zu achten, siehe meine Kommentare dort, soweit noch verfügbar).
Das fragliche Dokument ist hier:
https://wwwnc.cdc.gov/eid/article/26/6/20-0516_article
Nun stelle ich mir die Frage: wie soll denn aus dem Viren-Konglomerat, das so ein Nasen-/Rachen-Abstrich ohne Zweifel darstellt, ein einzelnes Virus isoliert werden? Mitgeschleppte Bakterien kann man ja wenigsten zurückdrängen. Aber Viren? ich lese hier (DeepL-Transl.):
“
„Zellkultur, Begrenzung der Verdünnung und Virusisolierung
Wir verwendeten Vero CCL-81-Zellen zur Isolierung und initialen Passage. Wir kultivierten Vero E6, Vero CCL-81, HUH 7.0, 293T, A549 und EFKB3-Zellen in Dulbecco Minimal Essential Medium (DMEM), ergänzt mit hitzeinaktiviertem fötalem Rinderserum (5% oder 10%) und Antibiotika/Antimykotika (GIBCO, https://www.thermofisher.comExternal Link). Wir verwendeten sowohl NP- als auch OP-Abstrichproben zur Virusisolierung. Zur Isolierung, Begrenzung der Verdünnung und Passage 1 des Virus pipettierten wir 50 μL serumfreies DMEM in die Spalten 2-12 einer 96-Well-Gewebekulturplatte, dann pipettierten wir 100 μL klinische Proben in Spalte 1 und verdünnten sie seriell 2-fach über die Platte. Dann trypsinierten und resuspendierten wir Vero-Zellen in DMEM, das 10% fötales Rinderserum, 2× Penicillin/Streptomycin, 2× Antibiotika/Antimykotika und 2× Amphotericin B in einer Konzentration von 2,5 × 105 Zellen/ml enthielt. Wir fügten 100 μL Zellsuspension direkt zu den Verdünnungen der klinischen Proben hinzu und mischten sie vorsichtig durch Pipettieren. Anschließend züchteten wir die beimpften Kulturen in einem befeuchteten 37°C-Brutschrank in einer Atmosphäre von 5% CO2 und beobachteten täglich zytopathische Effekte (CPEs). Wir verwendeten Standard-Plaque-Tests für SARS-CoV-2, die auf den Protokollen von SARS-CoV und dem Nahost-Coronavirus des respiratorischen Syndroms (MERS-CoV) basierten (9,10).“
und dann kommt’s:
„Wenn CPEs beobachtet wurden, schabten wir Zellmonolayer mit der Rückseite einer Pipettenspitze ab. Wir verwendeten 50 μL Viruslysat für die Gesamtnukleinsäureextraktion für Bestätigungstests und Sequenzierung. Wir verwendeten auch 50 μL Viruslysat, um eine Vertiefung einer zu 90% konfluenten 24-Well-Platte zu inokulieren.“
Übersetzt mit http://www.DeepL.com/Translator (kostenlose Version)“
Klar, ich habe davon keine Ahnung. Aber ich erkenne hier keinerlei Schritt, der aus dem Viren-Konglomerat ein bestimmtes auswählen, und nur dieses vermehren würde. Aber das beste ist das Abschaben des Zellmonolayers mit der Rückseite der Pipettenspitze. Das ist für mich wahre, hohe, genialistische Forschung! 😉
Übrigens habe ich ein mikrobiologisches Praktikum absolviert. Also völlig unbeleckt bin ich nicht. Bakterien kann man aufkonzentrieren, indem man aus einer Kultur möglichst wenig Material entnimmt, damit eine weiter Kultur anlegt, wenig Material entnimmt, Kultur anlegt, entnimmt, anlegt, … Dadurch wird das Zielbakterium immer weiter vereinzelt. Das ganze erfolgt per Hand auf Nährboden in Petrischalen und mithilfe eines Mikroskops.
Aber wie das für Viren gehen soll (die ja auf lebenden Zellen gezüchtet werden müssen) und vielfach kleiner sind als Bakterien (klar man sieht auch die einzelne Bakterie nicht im Lichtmikroskop, aber die Bakterien-Kultur)???? ich sehe nicht, wie man Virenbestandteile von Zellbestandteilen trennen soll – geschweige denn, wie man Viren vereinzelt bzw. eine „monovirale“ Kultur anlegen will.
Fragen über Fragen …
Ist mit Frank Drebbin der Moderator Mercury80 aus dem Heiseforum gemeint?
Unter diesem Account provoziert der alles und jeden und sperrt oder verschiebt zig Forenposts die sich kritisch mit den Corona-Maßnahmen auseinandersetzen. Diese „Person“ verteidigt die Regierungslinie bis aufs Messer. Angeblich ist das eine Frau, die einen Outdoor-Laden besitzt, nebenbei Rettungssanitäterin ist, mit einer Tochter, die auch Rettungssanitäterin oder Notärztin ist. Gleichzeitig übernimmt sie von Freitagabend bis Montagfrüh die Moderatorenaufgabe im Heiseforum.
Nebenbei erweckt sie den Eindruck, durch Selbststudium, auch noch Virologin zu sein.
Meiner Erinnerung nach wird direkt unter dem Namen „Frank Drebbin“ auch fleißig bei Telepolis kommentiert, und ja: straff nach dem Narrativ des Wahrheitsministeriums.
Grüße, Ped
Mein Post auf Telepolis wurde gesperrt, weil ich Drebbin als neuen Normalen bezeichnet habe.
Mit der Zeit lernt man die Account-Namen der Mainstream-Hass-Poster dort kennen. Ja nicht auf deren Niveau eingehen oder sich von denen provozieren lassen. Es ist schwer.
Wenn zum hundertsten mal Beleidigungen aus der untersten Schublade kommen – wenn zum tausendsten mal längst klar widerlegte Behauptungen aufgebracht werden als wenn sie so wahr wären wie die Sonne am Himmel … und wenn man sich zum zigsten male wundert, warum die Moderation gegen die einen so ignorant und gegen einen selbst so penetrant vorgeht.
Worauf ich mich nicht einlasse: mich verbiegen um der Gefahr des Gesperrt-Werdens zu entgehen. Genau das ist nämlich die Masche von solchen Blogs: die unbedarften Teilnehmer erziehen, die nützlichen hätscheln, die störenden entfernen.
Ach ja, „FrankDrebbin“ ist auch noch widerlegt:
„F_Drebbin“: „Da seit Mai Virenkulturen vom CDC allen Forschern zu Verfügung“
ich: „komisch dass das im Juni dann wieder nicht der Fall war:
„Since no
quantified virus isolates of the 2019-nCoV are currently available, assays designed for detection of the
2019-nCoV RNA were tested with characterized stocks of in vitro transcribed full length RNA (N gene;
GenBank accession: MN908947.2) of known titer (RNA copies/µL) spiked into a diluent consisting of a
suspension of human A549 cells and viral transport medium (VTM) to mimic clinical specimen. “
https://www.fda.gov/media/134922/download
Effective Date: 07/13/2020″
https://www.heise.de/forum/Telepolis/Kommentare/US-Studie-Vermehrte-Fahrten-zwischen-Landkreisen-erhoehen-Corona-Infektionszahlen/komisch-dass-das-im-Juni-dann-wieder-nicht-der-Fall-war/posting-37632860/show/
juckt so eine Flach-Pfeife natürlich nicht die Bohne
Kleiner Gag am Rande: Herr Drosten hat starke Beziehungen nach Russland Ohgottogott, RUSSIAGATE!)
nämlich zur Sechenov First Moscow State Medical University und zu vielen damit verbundenen Personen
Hier https://covid19.elsevierpure.com/en/persons/c-drosten/network/
die Option „Research Unit“ zuschalten.
Das Tool lädt zum spielen ein 🙂
man zieh zb die Moscow Uni zur Seite raus und das RKI zur anderen Seite …
Dazu noch so ein paar, wie ich meine, auffällig Findungen:
„Covid-19-Scopus“ listet zu „Coronavirus“ 8.690 Profile von Forschern. Nun kann ich das nicht vergleichen mit der Anzahl der Forschern, die an anderen Viren arbeiten, da dieses Covid-19-Scopus nur genau den Teil von Scopus öffentlich macht, der sich mit Covid befasst.
Aber irgendwie glaube ich nicht, dass es auch jeweils zu Rhinoviren, Adenoviren und wie sie alle heißen auch so viele Spezialisten gibt. Warum so viele zu Corona-Viren? Welche Studien begründen ein so massives Interesse an den Corona-Viren? Könnte ein Rhino-Virus nicht auch plötzlich mutieren oder von Tier auf Mensch springen und gefährlich für uns werden – wie ja die Geschichte um die heutige Pandemie geht?
6556 Forscher arbeiten schon länger am Thema, 2134 sind in den letzten 5 Jahren dazugekommen, also fast 25% Zuwachs
Relevanz:
1. Kwok yung Yuen
The University of Hong Kong mit 147 „Treffern“ (Veröffentlichungen und Kollaborationen sind wohl gemeint)
R. S. Baric
University of North Carolina at Chapel Hill mit 143 Treffer
Luis Enjuanes
CSIC
CSIC – National Center for Biotechnology mit 127 Treffern
S. Perlman
University of Iowa mit 122 Treffern
P. J. Rottier
Utrecht University 91 Treffer
und schon an weltweit 6. Stelle unser Star
6. Christian Drosten
Charité – Universitätsmedizin Berlin mit auch 91 Treffern
Kwok yung Yuen und Drosten sind die Jungstars, beide erst seit 2003 gelistet, die anderen schon seit 1981-1987. Also die beiden Superstars haben in 17 Jahren schon soviel oder mehr veröffentlicht und gemacht wie die führenden anderen jeweils in fast 40 Jahren.
Für mich sieht das so aus, wie wenn um die Jahrtausendwende etwas geschehen sein müsse, was aus einem in unseren Augen „normalen Virus“ neben all den anderen, ein ganz besonderes Virus machte, ein Virus, auf das man sich ungeheurer „Manpower“ und Energie stürzen müsse. Das „Middle East Respiratory Syndrome“ war es nicht, das trat 2012 auf. 2003 wurde das SARS-CoV1 entdeckt.
Die SARS-Pandemie 2002/2003 wies laut WIkipedia 8086 „Fälle“ auf mit 774 Toten WELTWEIT und über einen Verlauf über 7 Monate!
Das Muster ist dasselbe: angebliches erstes Aufkommen in China, Diagnose einer „attypischen Lungenentzündung“ und dann weltweite Verbreitung. Die Nachzeichnung mit inbrünstiger Sicherheit über den angeblichen Verbreitungsweg dieses Virus ist nachgerade lächerlich.
Auch hier das gleiche vorgehen. ein Drosten-Test der irgendwas anzeigt – keiner weiß genau, was.
„Als erste Pandemie des 21. Jahrhunderts weckte sie neue Ängste in der Bevölkerung und wurde weltweit in großem Rahmen von den Medien begleitet. Ihr erlagen außerhalb Asiens 45 Menschen[2] und sie ist ein warnendes Beispiel für die rasche Ausbreitung einer Krankheit in der vernetzten, globalisierten Welt.“
Die Blaupause für das heutige Geschehen. man denke immer daran: angeblich bestätigte Tote: 774, in Worten siebenhundertvierundsiebzig! Weltweit, und über eine Zeitraum von 7 Monate! Ein Zeitraum in dem über 32 Millionen Menschen an allen möglichen aufgeklärten und unaufgeklärten Ursachen gestorben sind! Und über diese 774 von 32.000.000 Toten weltweit will man also genau Bescheid wissen? Das ist Kindergarten-Wissenschaft auf unterstem Niveau.
https://de.wikipedia.org/wiki/SARS-Pandemie_2002/2003
Ped, Ihre Blog-Software verschluckt leider Nummerierungen. Von erstens bis sechstens blieb nur noch erstens und sechstens.
Baric auf zweiter Stelle, Enjuanes dritte Stelle, Perlman vierte, Rottier fünfte (Kopf an Kopf mit Drostilein)
Es wird nur bis zur fünften Ebene in den Kommentaren verschachtelt 😉
Grüße, Ped
Neene, das war keine Verschachtelung sondern formatfreies 1., 2., 3., …, das wird zerlegt, genau so wie „Bulletpoints“ zb mit „Minuszeichen“ am Zeilenanfang. Deshalb bin ich bei Bedarf auf Unterstrich am Zeilenanfang gegangen. Das kommt normal durch.
Da liegt Markdown drunter:
Nun, Paul Schreyer und sein neues Buch dürfte auch Ihnen nicht entgangen sein und seine Recherchen zu Verknüpfungen von Stiftungen, Multioligarchen, Pandmie Übungsszenarien über Pharma Industrie hin zur Verschmelzung mit Regierungen, allen voran, Bill Gates
Wie schaut es aber nun mit der Bekanntheit von Herrn Haering aus?
Immerhin der, der sich schon sehr lange mit der Bargeld Abschaffung beschäftigt und über welche Organisationen das vorangetrieben wird, die Beleuchtung des WEF und des Herrn Klaus Schwab?
ID 2020 sollte doch ein Begriff sein, oder nicht?
Falls nicht, einfach mal lesen, damit auseinandersetzen und vielleicht auch mal bei der Radio Sendung des SRF Schweiz reinhören.
Das ist das Bild, wie alles zusammenläuft und den “ great Reset “ ausmacht und was die neue Weltordnung bedeutet, die „neue Normalität, die man uns nicht verkauft, aber mit der Corona Krise hinten einstielt.
Ist das die Vorstellung einer zukünftigen Welt?
Wollen Wir das so leben?
Glauben jemand, das trifft ihn nicht, weil er zu den Guten und Reichen und Schönen gehöret?
Möchten wir zukünftig so unfrei leben, oder ist es egal, weil diese Unfreiheit nur andere betrifft?
Schöne heile Welt, die man uns da präsentiert, oder?
Viele Alternativen haben wir nicht mehr, um das so nicht zuzulassen.
Es wird ein unvorstellbarer Kampf werden.
Werden wir diesen auch führen?
Ich zumindest hoffe sehr, alleine lasse ich dabei keinen, insofern alle kämpfen, denn alleine ist man verloren.
Aber jetzt geht es erst los, alles bis hier hin war nur Vorbereitung.
Gehen wir den Weg, vermutlich weniger in, aber dafür mehr für FREIHEIT, FRIEDEN und LIEBE.
https://youtu.be/2HWo0RJ3eYI
https://norberthaering.de/die-regenten-der-welt/commonspass/
https://norberthaering.de/die-regenten-der-welt/srf-id2020/
https://www.srf.ch/play/radio/kontext/audio/globale-e-id-initiativen—ihre-moeglichkeiten-und-grenzen?id=83db5967-74ff-4cf7-b22a-d7aa7ee712e5
wenn alle menschen getestet/geimpft wurden und alle daten/profile auf einem server in den usa vorliegen kann man einschätzen wie groß der widerstand bei der abschaffung der demokratien sein könnte, in China hat man das volk schon im griff—die chinesen glauben nicht an die allmacht gottes aber an die allmacht der partei—die WHO will keinen weltweiten wirtschaftslockdown mehr um die chinesischen absatzmärkte nicht zu gefährden, also verordnet man nur einen freizeitlockdown, d.h. die weltbevölkerung wird daran gewöhnt nur noch für die arbeit/familie zu leben das kommt einer klerikalisierung/chinesische versklavung gleich—die weltweiten regierungen lassen die leinen der rechts-/linksradikalen locker um einen sturz der demokratien herbeizuführen—man versucht die französische revolution/aufklärung rückgängig zu machen und die weltbevölkerung zu versklaven